Energy and Power.
The world is shifting away from energy sources that produce carbon and other greenhouse gases to preserve Earth’s climate. However, such emissions are of no concern on the Moon or Mars. The Moon has no atmosphere to trap these gases, and Mars possesses only a thin atmosphere. In the latter case, greenhouse gas emissions would actively warm the cold planet, aiding in planned martian terraforming efforts.
Internal combustion is a very well-understood piece of engineering technology. But, largely due to the issues discussed above, internal combustion engines (ICE) are fading from the realm of technological advancement. In their place, carbon-free technologies — including photovoltaic, nuclear, and fuel cells — are undergoing rapid technological evolution. Due to this widespread development, scientists and engineers are also integrating these carbon-free technologies into future space applications. In some cases, without a proper evaluation of all possible solutions. However, the advantages of ICE over other sources of energy are abundantly clear!
There are three primary considerations when choosing an energy source for space applications. First, it is always essential to consider mass, as moving larger loads leads to higher launch costs and increased technical difficulties. Another cost factor is the number of precautions taken to transport the launch cargo safely. For example, batteries and nuclear require extensive testing before they are permitted to fly due to the fire and environmental hazards that they pose. An ICE that runs on the same fuel as the rocket can launch “dry,” minimizing potential risks. Lastly, it is important to consider power and energy outputs. We can compare different technology options by weighing their power and energy densities.
The image above gives an analogy to thinking about what power and energy density means. Energy is the ability for something to do work and can be related to the total volume of liquid in the bottle. Power is the rate at which energy can be expended and is analogous to the flow rate out of the bottle.
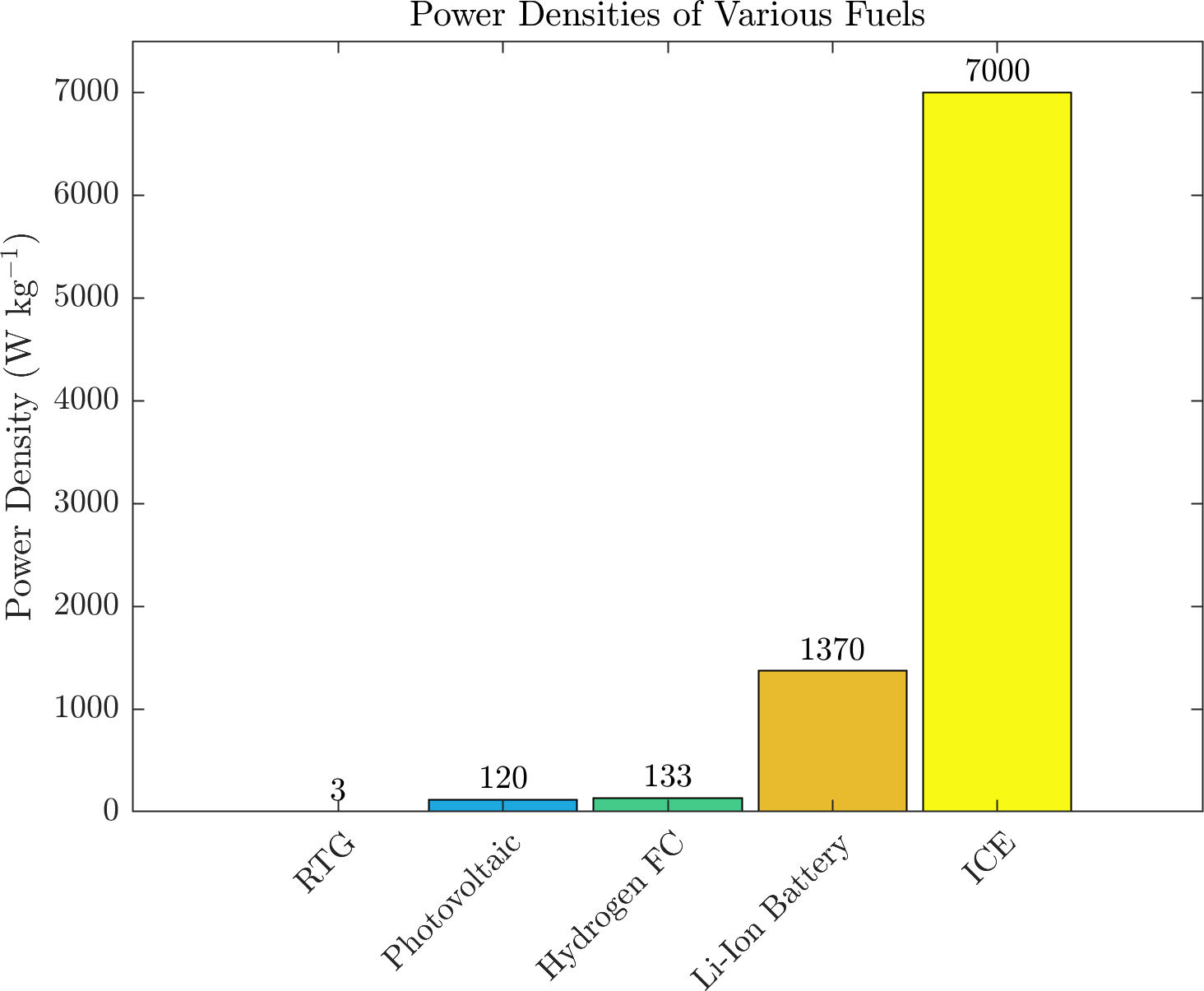
how Combustion stacks up
Early development of Lunar and Martian bases will require energy sources with ample power output in mobile packages. We can look at the power to mass ratios of different technologies to evaluate this.
Radioisotope Thermoelectric Generators (source) – NASA’s eMMRTG produces 140 W at its peak, slowly dropping off as the plutonium decays. The device weighs 45 kg, yielding a power-to-mass ratio of approximately 3 W/kg. This power output is too low for operating something like drilling equipment. This source is most fitted for low-power demand applications like small, unoccupied rovers (power to excavate).
Photovoltaic (source) – To match the same power output of the eMMRTG mentioned above, a solar equivalent would weigh 442 kg. Solar arrays can collect decent amounts of energy but still need a battery to store the accumulated energy. Solar panels are also prone to loss of efficiency from damage or collection of dust on the solar cells. Furthermore, NASA will conduct the initial Lunar missions at the poles, where sunlight is absent. Relying on solar flux as distance increases from the sun is also a problem. Since solar power is proportional to the inverse square of the distance, Mars solar panels would lose 40% of their effectiveness compared to those on Earth.
Fuel Cells (source) – Fuel cell technology is still being perfected, but it has been deployed successfully on space missions since the Apollo era. A modern example would be the alkaline fuel cells used on the Space Shuttle Orbiter, which produced 12 kW of continuous power in a device that weighs 90 kg, coming out only around 133 W/kg for its power density.
Batteries – Impressive numbers have come from the recent Tesla batteries (source). Take, for example, their 75 kWh battery, weighing roughly 544 kg and producing over 1000 hp (745 kW). As a result, Tesla’s drive unit has a power density of 1370 W/kg and is the only option that comes close to internal combustion engines in terms of power, but there is a catch. The energy density is roughly 137 W-h/kg, which means if you throttle this battery to full power, it will last only six minutes. Another shortcoming is the sharp drop-off in performance of batteries in cold temperatures, and you sure can bet the Moon and Mars will be cold.
Internal Combustion
Combustion engines have been dominant since the late 1800s on Earth because fossil fuels are so energy-dense. After accounting for the weight of a fueled gas tank, the average road car engine has no problem reaching power densities of 1200–1500 W/kg.
Despite the efficiency of today’s ICEs being around 30%, the useable power output from the fuel is still relatively high. Moreover, the performance racing world, where high power-to-weight ratios are critical, shows even more promising numbers. Take, for example, the Nissan DIG-T R engine, which puts out 400 hp (29,8280 W) in a 40 kg package, netting an impressive 7457 W/kg (source)!
So far, we have shown how the power output of petrol engines is the most advantageous, but what about their energy density? Under optimal operating conditions, battery-electric cars are only starting to be on par with gasoline cars. On Earth, gasoline is convenient because it is energy-dense, liquid at room temperature, and combusts with the oxygen present in the air. However, there are more energetic fuel sources, such as the cryogenic bipropellants used for rockets.
| Bipropellant | Gravimetric Energy Density (W-hr/kg) |
Volumetric Energy Density (W-hr/L) |
|---|---|---|
| Hydrogen/Carbon Dioxide (H/CO2) | 25,833 | 416 |
| Hydrazine/Carbon Dioxide (N2H4/CO2) | 1,329 | 1,111 |
| Hydrogen/Oxygen (H/O2) | 3,750 | 1,312 |
| Carbon/Monoxide (C/O) | 1,816 | 2,144 |
| Methanol/Oxygen (CH3OH/O2) | 2,129 | 2,093 |
| Methane/Oxygen (CH4/O2) | 2,800 | 2,380 |
Numbers derived from heat of formulation (enthalpy) on a molar basis.
Take Methane, for example. With an energy density of 2,800 W-hr/kg, this fuel will carry astronauts back to the Moon in 2024. A VOICE, operating at 30% efficiency, would weigh 500 kg and produce the same 1000 hp as the Tesla battery. Suppose a methane/oxygen bipropellant engine had a power density of 5000 W/kg, which is far less than the already achieved Nissan DIG-T R. This engine could output 1000 useable horsepower for over 30 minutes on a single kilogram of fuel. Therefore, a single kilogram of methane/oxygen bipropellant, running in an engine weighing 44 kg less than the Tesla battery, can run at full power for five times longer than the same fully charged battery. A VOICE vehicle would have many kilograms of fuel, allowing for a powerful and enduring operational run time far beyond batteries.